He gives his purpose for the first book right at the beginning:
The object of this little book is to furnish evidence, first, that it is essential, for the purpose of teaching or examining in elementary Geometry, to employ one textbook only; secondly, that there are strong a priori reasons for retaining, in all its main features, and specially in its sequence and numbering of Propositions and in its treatment of Parallels, the Manual of Euclid; and thirdly, that no sufficient reasons have yet been shown for abandoning it in favour of any one of the modern Manuals which have been offered as substitutes.
It is written in the form of a satirical dialogue between Minos and Rhadamanthus, both of whom are examiners treating modern textbooks like examination papers, the Phantasm of Euclid, and Professor Niemand, the counsel for the modern would-be replacements. Minos's description is perfect: "His hair, from much running of fingers through it, radiates in all directions, and surrounds his head like a halo of glory, or like the second Corollary of Euclid I.32." The second Corollary of I.32 is "All the exterior angles of any rectilineal figure are together equal to four right angles", and in Todhunter the diagram for it is:
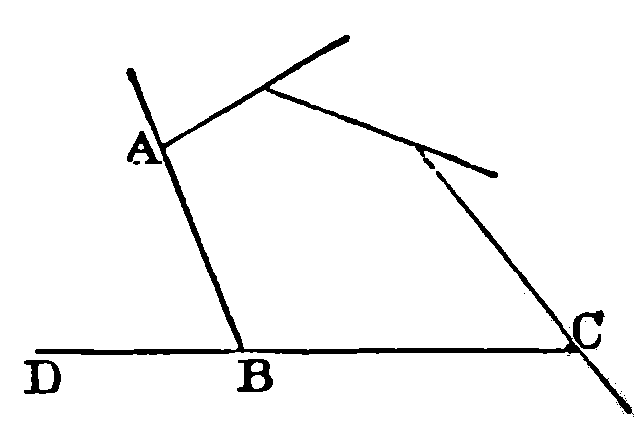
One of Carroll's consistent points throughout is that for a geometry textbook you are not actually presenting geometry itself; what you want is "a book that will exercise the learner in habits of clear definite conception, and enable him to test the logical value of a scientific argument", as Minos tells the Phantasm of Euclid. Thus it is irrelevant whether there are omissions; overloading the curriculum is a danger to be avoided, and, in any case, if it's just a matter of adding a few theorems that have turned out to be especially useful, adding such things to Euclid is something that geometry teachers have always done. In addition, you want a clear line of inferences. While there are many cases in which you could do something in a different order than Euclid does, for teaching beginners, this is not something you should be getting into, and Euclid, having been a standard reference for so long, provides the service of a universal reference, with a numbering system on which everyone can agree.
Carroll regards only two of the criticisms of Euclid to be of any significance: the criticism that Euclid does not distinguish problems from theorems (which had been proposed as a major criticism in Carroll's day), and the criticism of Euclid's treatment of parallels. The former Carroll seems to find easily answered (separating problems and theorems doesn't actually seem to provide any improvement for the teaching of beginners), and most of the book is concerned with the latter. Part of the complexity of the latter is perhaps due to the fact that Carroll thinks axioms have to be established as axioms -- as Euclid tells Minos in discussing Playfair's Axiom, "What is an Axiom at one stage of our knowledge is often anything but an Axiom at an earlier stage" -- so to determine what should count as axiom, you need to lay out what it is useful for proving within a system and determine how it meets the several requirements for what you are trying to do. And, of course, in teaching geometry, one of the requirements is that it be suitable for beginners, that is, that it be something that can be grasped and used without a developed sense of geometrical constructions or proof techniques; most modern treatments Carroll thinks get tempted off the right pedagogical road by pursuit of a standard of elegance or rigor that raises the difficulty, without increasing clarity, for people just starting out.
Carroll had no problem with doing things differently from Euclid, however, as long as you didn't try to overcomplicate beginner's work with it, and he himself devoted a considerable amount of thought to different ways of handling parallels. One way is found in his Curiosa Mathematica, Part I -- or, actually two ways, since in his original version he used a hexagon in his substitute for Euclid's parallel postulate, but decided instead to simplify it further in the third edition to a tetragon. Part of what Carroll wanted to do was come up with a substitute for Euclid's treatment of the parallels that did not, like almost all other proposed at the time, involve infinities or infinitesimals in one way or another, but just used basic ideas easily accessible to human reason. His proposed substitute is, "In any Circle, the inscribed Tetragon is greater than any one of the Segments that lie outside it."
A great many people wonder why Carroll, so creative, shows little interest in non-Euclidean geometries; but, of course, even today non-Euclidean geometries are not what you think about for teaching people just starting out, so one wouldn't expect it to arise in the context of his work on mathematical pedagogy. As for the geometrical work itself, though, Carroll quite clearly regards Euclidean geometry as true, and thus the primary issue as one of finding the best foundations for a Euclidean geometry. It's also worth recalling -- mathematicians in particular tend to forget it when thinking about the history of mathematics -- that mathematical results do not propagate instantaneously, and prior to the twentieth century, they propagated very slowly indeed across national lines. People kept up with international work, as they could, but people in different nations often didn't share the same notations, teach the same methods, or prefer the same approaches. Carroll, even if he had not simply thought it a bunch of clever paradoxes, could have been aware of the work on non-Euclidean geometry without having had the kind of access to it that would have made it possible for him to work on the subject without essentially starting from scratch himself or devoting several years of his life to researching it.